Copyright © Cay S. Horstmann 2011
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License.

Parsing 5

Grammar techniques
Repetition
Precedence and associativity
LL(1) grammars
Avoiding left recursion
Left factoring
Ambiguity

Reminder: Context-Free Grammar

Productions

expr ::= term (( "+" | "-" ) expr)?
term ::= factor (( "*" | "/" ) term)?
factor ::= wholeNumber | "(" expr ")"

Non-terminals expr term factor
Terminals (tokens) wholeNumber "(" "+" ...
Parse tree shows derivation process

Repetition

Simple repetition, ex. array bounds [10][10][20]

bounds ::= bound | bound bounds
bound = "[" number "]"

Or in EBNF
```
bounds ::= (bound)+
```

In Scala, simply collect all

def bounds = bound ~ rep(bound) ^^ { case head ~ tail => head :: tail }
bound = "[" ~> number <~ "]" ^^ { _.toInt }

Or use rep1 convenience combinator
```
def bounds = rep1(bound)
```
No transform needed
Repetition with separators, ex. function arguments id(arg1, arg2, ...)
```
funcall ::= ident ~ "(" ~ expr ("," expr)* ")"
```
Scala convenience combinator
```
def funcall = ident ~ "(" ~> repsep(expr, ",") <~ ")"
```
repsep returns List without separators; here, List[Expr]

Operator Precedence

Term/factor levels make * / stronger than + -:

expr ::= term (( "+" | "-" ) expr)?
term ::= factor (( "*" | "/" ) term)?
factor ::= wholeNumber | "(" expr ")"

Even stronger operator, say ^ for “raise to a power”

term ::= factor (( "*" | "/" ) term)?
factor ::= factor1 ( "^" factor )?
factor1 ::= wholeNumber | "(" expr ")"

Weaker operator, say == <>

expr ::= expr1 (( "==" | "<>" ) expr)?
expr1 ::= term (( "+" | "-" ) expr1)?
term ::= factor (( "*" | "/" ) term)?
factor ::= wholeNumber | "(" expr ")"

Operator Associativity

Right recursion is naturally right associative

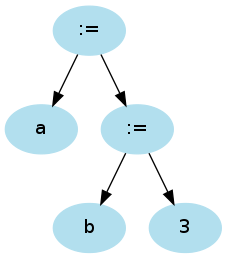
assignment ::= ident ":=" assignment | ident ":=" expr

For example,
```
a := b := 3
```
parses as
Left recursion is naturally left recursive, but undesirable for us
See below for remedy

LL(1) Grammars

Start from the grammar root
Apply productions until input string is reached
Which production?
With some grammars, choice can be deterministic
Desirable to have one-token lookahead property, called LL(1): Only one production can be chosen depending on the next token
Example: 3 + 4 * 5
Start from grammar root: expr ::= term (( "+" | "-" ) expr)?
After matching 3 as term → factor → wholeNumber, back in term:
```
term ::= factor 
term ::= factor ("*" | "/") term
```
Should we go on with ("*" | "/") term? No—next token is "+"

Avoiding Left Recursion

A grammar rule is left recursive if the left hand side appears at the beginning of the right hand side
```
expr ::= expr "+" term | term
```
Not LL(1) because there is no way of choosing between the two rules
Infinite recursion in Scala combinator parser
Can be removed by observing that eventually expr must be a term
```
expr ::= term | term rest
rest ::= "+" term rest
```
Annoyance: Right recursion not convenient for left-associative operators

Scala solution: Collect all terms and fold

def expr = term ~ rep("+" ~> term) ^^ 
  { case a ~ lst =>  (a /: lst) { Sum(_, _) } }

(See previous lecture for details)

Left recursion is not a problem for bottom-up parsers (which we don't discuss in this class)

Left Factoring

If a grammar has rules of the form
```
A ::= α β | α γ
```
it can't be LL(1)
Example:
Assignment statement and procedure call both start with identifier
```
stat ::= ident ":=" expr | ident "(" expr ("," expr)* ")" | ...
```

Factor out common left

stat ::= ident rest | ...
rest ::= ":=" expr | "(" expr ("," expr)* ")"

Annoyance: Complicates semantic analysis because identifier is separated from assignment or call

Scala solution: opt and match

def stat = ident ~ (":=" expr | "(" expr ")")

Ambiguity

if with optional else

ifstat ::= "if" "(" expr ")" stat ("else" stat)?

Gives rise to ambiguous construct
```
if (c1) if (c2) s1 else s2
```
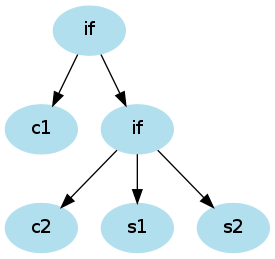or
Disambiguation depends on parser technology
Scala: The obvious rule gives the expected behavior (see Lab)
```
(("if" ~ "(") ~> expr <~ ")") ~ stat ~ opt("else" ~> expr)
```

Reading Grammars

Useful skill, even outside programming language theory
E.g. to determine correct file formats
Variation in grammar syntax
Terminals vs. nonterminals—some authors enclose nonterminals in <...>
```
<expr> ::= <term> | <term> (+ | -) <expr>
```
Then no "..." around terminals
[...], {...} instead of (...)?, (...)*

Lab

One of you writes the code, the other types up answers
Switch coder/scribe roles each lab
Submit lab work to Sakai.

Step 1

Look at the Annotated XML Specification Section 3.1. Can you have spaces before an element name in a start tag?
```
< name>
```
Which grammar rule did you use to answer this question?
Before the /> in an empty-element tag?
```
<name />
```
Which grammar rule did you use to answer this question?
Around the = in an attribute?
```
<name attr = "value">
```
Which grammar rule did you use to answer this question?

Step 2

Design a grammar for the function headers of Crazy Section 2.4 (without the body). Write the grammar in EBNF form.
Write a Scala program that parses a Crazy function header, using a Parser[Any]. What is your program? What output do you get for
```
function area(a: integer; b: real; c: integer): real; 
```
For
```
function area(a: integer; b, c: real): real; 
```
Improve your program to yield a Function object, defined below:
```
case class Variable(name : String, `type` : String) 
  // type is a reserved word in Scala. 
  // We use `...` to parse it as an identifier
case class Function(name : String, params : List[Variable], returnType : String)
```
Do only the easy part, where all params have the form repsep(param, ";") where param is ident ~ ":" ~ ident. That is, don't yet handle parameter groups of the form a, b : type. (You'll do that later in the term project.)

What is your program? What output do you get for
```
function area(a: integer; b: real; c: integer): real; 
```
Hint: Transform parameters into Variable objects
```
def param: Parser[Variable] = ident ~ (":" ~> ident) ^^ 
  { case i ~ t => Variable(i, t) }
```
Hint: You always want to use ~> and <~ to throw away tokens. But you often need parentheses. Note that ~, ~>, and <- are left associative and <- has lower precedence than ~, ~>.For example,
```
ident ~ (":" ~> ident)
```
or
```
(ident <~ ":") ~ ident
```

Step 3 (Optional)

Write a Scala parser for the grammar
```
expr ::= "if" "(" number ")" expr ("else" expr)? | number
```
What is your program? What do you get when you parse
```
if (1) if (2) 3 else 4
```

Ok, it's too tedious to figure out whether the else associates with the first or second if. Enhance your program to yield a IfExpr. Use the following outline:

class Expr
case class IfExpr(cond : Number, pos : Expr, neg : Expr) extends Expr
case class Number(value : String) extends Expr

class SimpleLanguageParser extends JavaTokenParsers {    
  def expr: Parser[Expr] = ... 
  def number: Parser[Number] = wholeNumber ^^ { Number(_) }
}

Transform cond ~ expr ~ None into IfExpr(cond, expr, null).

Now what do you get for

if (1) if (2) 3 else 4

Does the Scala parser resolve the if/if/else ambiguity in the same way as C++, or the other way?